こんにちは！ブレインズコンサルティングの大下です。

今回は、「あの論文を検証してみた！」のシリーズ第６回、A Structural Probe for Finding Syntax in Word Representationsを検証していきます。 BERT、ELMo で埋め込んだ空間表現の中に、パースツリー情報が埋め込まれているらしいことを示した論文です。本当に埋め込まれていると言ってよいのか、具体的にどのようにして構造を復元しているのかが疑問になるところです。

検証環境

まずは、動作確認に使った検証環境を明記しておきます。

Ubuntu 18.04.1 LTS (Bionic Beaver)
- CPU: Intel(R) Core(TM) i7-6700K CPU @ 4.00GHz / 4 cores / 8 processors
- Memory: 48GiB
- HDD: 約190GiB （Available なサイズ）
Python 3.6.5
PyCharm-community-2019.1.1
PyTorch 1.0.0

本検証におけるアウトプット

コード

スクリプト

参考

Excel(conllu)

スクリプト実行例

$ tar xzf structural-probes-bin.tar.gz
$ git clone https://github.com/john-hewitt/structural-probes.git
$ cd structural-probes
$ sh download_example.sh    # about for less 1 minuite.

スクリプトの構成概要

f:id:bci-oshita:20190425134000p:plain — shell_script

experiment

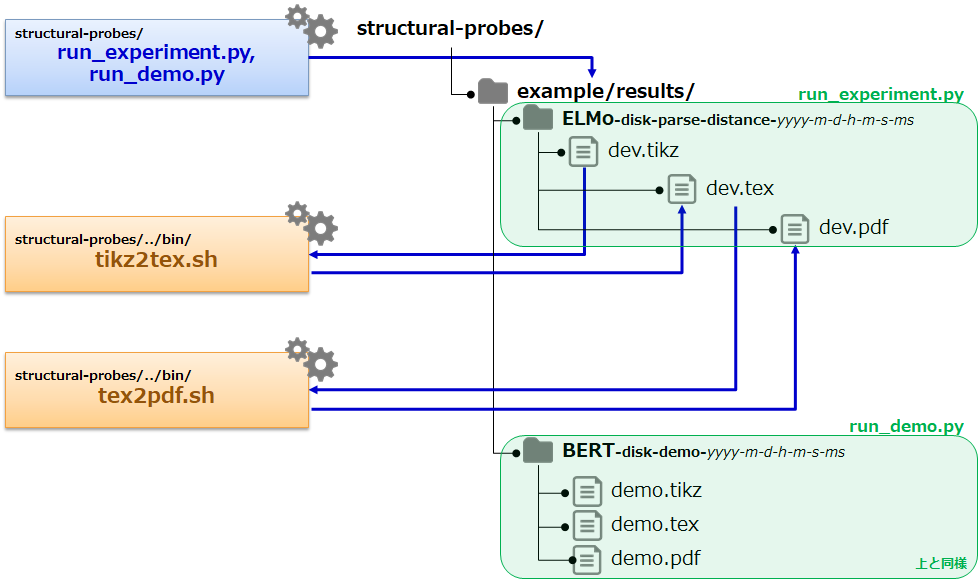
ELMo を使った実験スクリプトの実行例です。

distance ベース

$ sh ../bin/run_experiment.sh

※ 出力は、example/results/ELMo-disk-parse-distance-2019-4-25-13-55-17-321028/ のようなディレクトリに出力されます。

depth ベース

$ sh ../bin/run_experiment.sh --depth

※ 出力は、example/results/ELMo-disk-parse-depth-2019-4-25-14-2-54-227092/ のようなディレクトリに出力されます。

run_experiment.py の構成概要

f:id:bci-oshita:20190425132939p:plain — run_experiment.py

demo

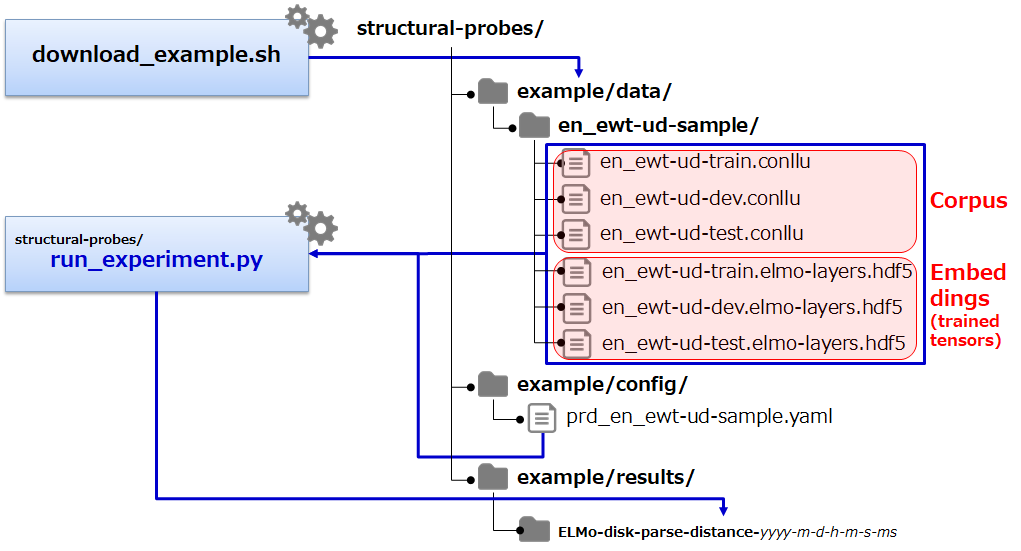
BERT-Large を使ったデモスクリプトの実行例です。

demo の実行

$ sh ../bin/run_demo.sh

※ 出力は、example/results/BERT-disk-demo-2019-4-25-13-56-55-19245/ のようなディレクトリに出力されます。

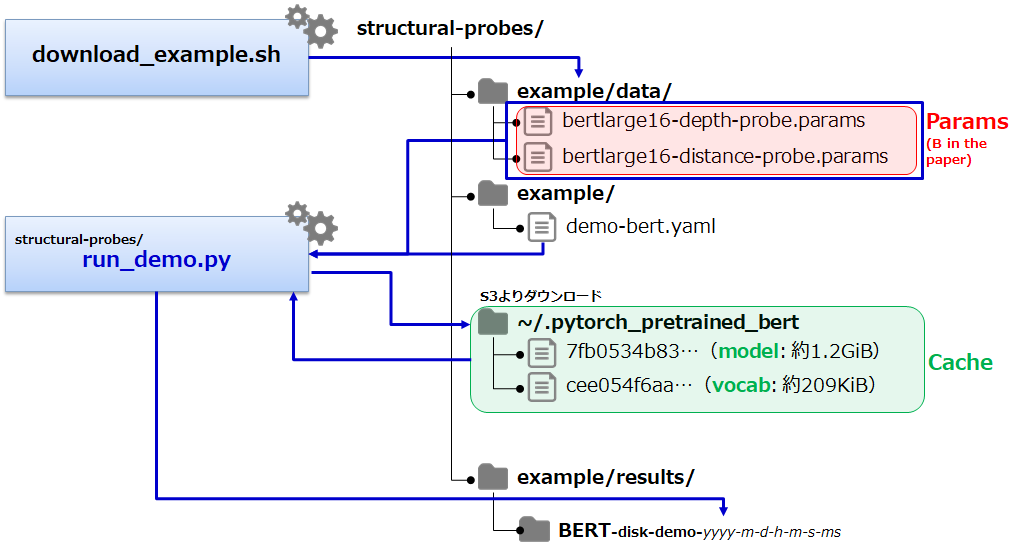
BERT-Largeのmodel、vocabをダウンロード

BERT-Large のmodel、vocab ファイルを個別に確認したい場合など、以下のスクリプトでダウンロードして確認することもできます。

$ sh ../bin/get_berts.sh
$ ls bert-large-cased-vocab.txt bert-large-cased.tar.gz
bert-large-cased-vocab.txt  bert-large-cased.tar.gz

※ run_demo.py でダウンロードされる場合は、~/.pytorch_pretrained_bert/ 配下に、ファイル名がハッシュ化されて保存されます。

run_demo.py の構成概要

f:id:bci-oshita:20190425133010p:plain — run_demo.py

概要

本記事が対象とする論文（structural-probes）の提案手法は、非常にシンプルで、 BERT, ELMo により埋め込まれたベクトルから各文（sentence）の構文木を生成するための線形写像を学習させる手法です。（その評価についても、提案されています。）

発想としては、グラフ構造がベクトル空間に埋め込まれていると考えると、距離（distance）、ノルム（norm==depth）が定義できるハズで、その距離、ノルムがグラフにおける近似としても扱えるであろうということです。

ということで、論文structural-probes では、2つのprobe が提案されています。１つは、the structural probe と呼ぶ、距離（distance）を使ったprobe もう一つは、tree depth structural probe と呼ぶ、ノルム（depth）を使ったprobeです。

準備

任意の $k \times m$ 行列 $B \in \mathbb{R}^{k \times m}$ は、 $B: \mathbb{R}^m \rightarrow \mathbb{R}^k$ のように、 $m$ 次元から $k$ 次元への線形写像としても見られます。

ここで、 $\| \cdot \|$ を、 $B$ で写された先のベクトル空間 $\mathbb{R}^k$ 上のノルム（実空間上で自然に定義できるノルム）とすると、

\begin{align} (Bh)^{\mathsf{T}} Bh = \| Bh \|^2 \end{align}

と表現できることに注目しておきます。（定義のまま）

The structural probe

線形写像 $B$ （probe 用のニューラルネットワークの重み/学習パラメータ）に対して、距離を定義します。

線形写像 $B$ が与えられた下で、文 $s$ 内の単語i, j に対する埋め込みベクトル（隠れ層のベクトル）、 $h_i, h_j$ に対して、距離を以下のように定義します。

\begin{align} d_B(h_i, h_j) = ( B(h_i - h_j)^{\mathsf{T}} ) ( B(h_i - h_j) ) \end{align}

$d(\cdot, \cdot)$ を、 $\mathbb{R}^k$ 上の距離（ノルムから定義された距離）とすると以下のように変形できます。

\begin{align} d_B(h_i, h_j) &= ( B(h_i - h_j)^{\mathsf{T}} ) ( B(h_i - h_j) ) \\ &= (Bh_i - Bh_j)^{\mathsf{T}} (Bh_i - Bh_j) \\ &= \| Bh_i - Bh_j \|^{2} \\ &= d(Bh_i, Bh_j)^{2} \\ \end{align}

ここで、この定義による $d_B(\cdot, \cdot)$ は、数学的な距離ではありません。（劣加法性を一般に示せない）ただ、論文に注釈がありますが、 $d(\cdot, \cdot)^{2}$ 、 $d(\cdot, \cdot)$ のいずれで定義した場合でも、今回の学習結果に大きな差がないとのことです。（つまり、学習する上では、2点間の距離感がわかればよく、当該論文の分析・評価においても、ベクトルの合成を踏まえた分析・評価をしないため。）

最適化

上記、距離の定義を使って、以下の最適化問題をニューラルネットワークで解くことになります。

各文 $s$ に対して、以下のような損失（誤差） $err_s$ を考える

\begin{align} err_s := \sum_{w_i, w_j \in s} | d_{Ts}(w_i, w_j) - d_B(h_i, h_j)^{2} | \end{align} ただし、 $w_i, w_j$ は、文 $s$ を構成する $i$ 番目または、 $j$ 番目の単語（サブ単語）とし、それぞれ対応する埋め込みベクトル（隠れ層のベクトル）を、 $h_i, h_j$ とする。

\begin{align} loss_B := \sum_s \frac{1}{|s|^{2}} err_s \end{align} ここで、 $|s|$ を、文 $s$ の長さ（単語/サブ単語の数）とする。（上式では、距離を考えるため、2乗することで正規化する）

学習パラメータ $B$ を学習することで、上記 $loss_B$ を最小化する。

\begin{align} \min_B loss_B \end{align}

木構造の復元方法

各単語ノード間の距離行列を使って、MST（Minimum Spanning Tree）アルゴリズムを使って、木構造を抽出します。 MST は、ざっくりいうと、すべての単語ノードをたどり、最小の枝コスト（ここでは、距離）になるように選出された木構造です。

structural-probes/reporter.py のprims_matrix_to_edges() メソッドとして実装されていますので、アルゴリズムの詳細は、ご確認いただければと思います。

木構造の評価

距離を最適化することにより得られた木構造に対して、UUAS(Undirected Unlabeled Attachment Score) により評価する。 UUAS は、評価用のデータセットの全ての文に対する、正解枝数 / 全枝数で計算する。

\begin{align} UUAS := \frac{\sum_s \texttt{correct_edges}_{s}}{\sum_s \texttt{total_edges}_{s}} \end{align}

Tree depth structural probe

木構造のdepth は、そのままで、root ノードから対象の単語ノードまでのedge の数として定義します。ベクトル空間上のノルムとみなして、最適化します。

（参考）CoNLL-U Format

run_experiment.py の入力（文集合）には、conllu ファイルが使われています。フォーマットの詳細は、CoNLL-U Format を参照ください。

conllu ファイルは、download_example.sh を実行すると以下に配置されます。

$ ls example/data/en_ewt-ud-sample/*conllu
example/data/en_ewt-ud-sample/en_ewt-ud-dev.conllu  example/data/en_ewt-ud-sample/en_ewt-ud-test.conllu  example/data/en_ewt-ud-sample/en_ewt-ud-train.conllu

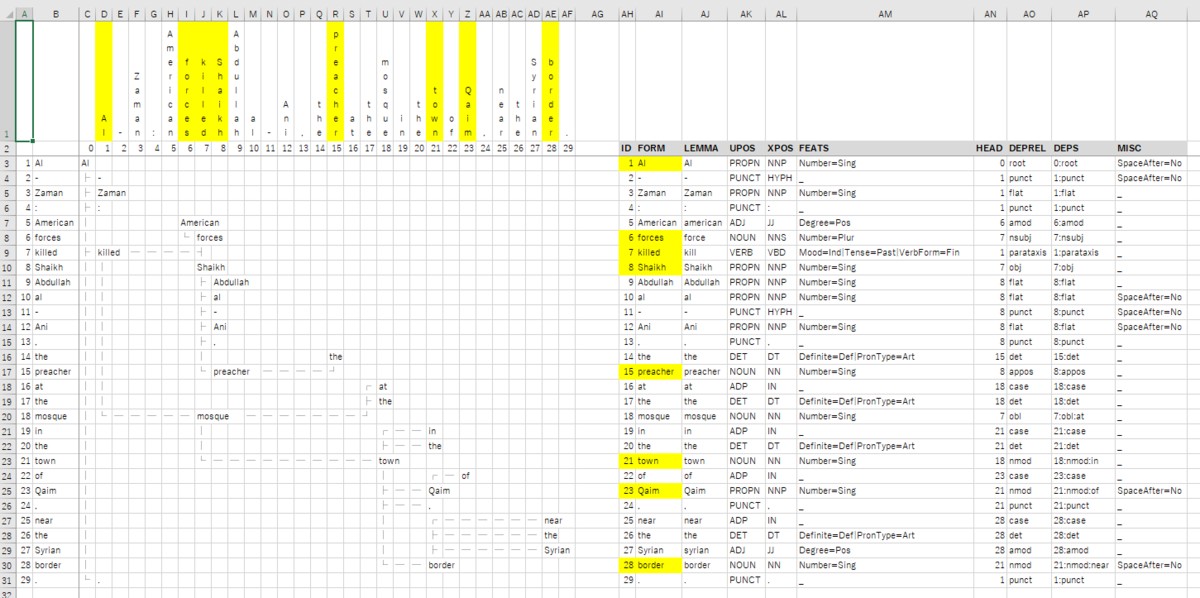
conllu ファイル内の1つの文（en_ewt-ud-train.conllu 内の最初の文）をサンプルに、木構造を再現すると以下のような感じになります。（地道にHEAD項目をたどっていくと作成できます。）

f:id:bci-oshita:20190425155200p:plain — conllu

グラフと考察

論文に記載されているグラフを見てみます。

各層のUUAS

論文に、各層に対するUUAS指標値がプロットされています。

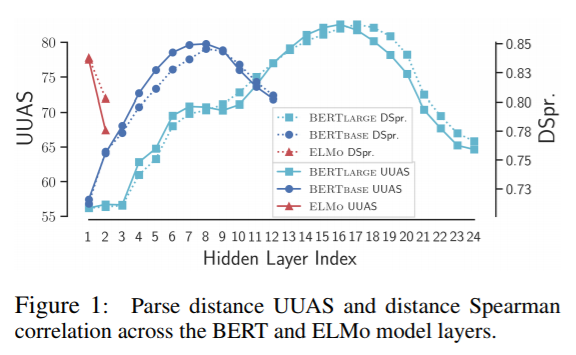
f:id:bci-oshita:20190425164638p:plain — parse-distance-uuas

BERT Base と BERT Large を比較すると、BERT Base のグラフを倍率（解像度）を上げたのが、BERT Large のようにも見えます。実際、UUASのピークが共に全層の2/3 のところ（=8/12, 16/24）に位置しています。（偶然かどうかは、確認できませんが。）つまり、UUASという指標値の視点では、層を増やすことが分解能を上げる（粒度を細かくする/精緻化する）ことに関係しているようにも見えます。（これは、Deep にすることで、精度が上がるという効果と違和感がない解釈です。）このことを拡大解釈すると、あるタスクを各層で分解（役割分担）しているとも考えられます。これが、BERT独自の性質なのか、ある程度の汎化性があるpre-train モデル全般に言えることかの調査は、興味深いと思います。

UUASと次元 $k$ の関係

次に、構文を表現する次元数 $k$ とaccuracy の関係を見てみます。ここで、 $k$ は、線形写像 $B$ で写した先

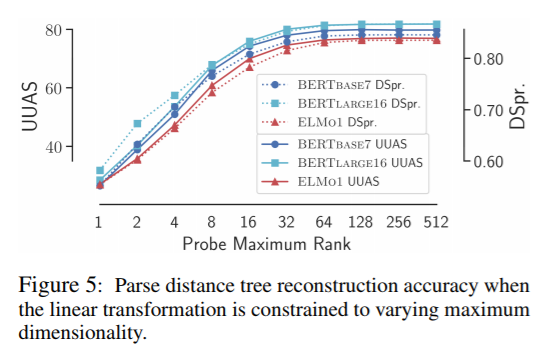
f:id:bci-oshita:20190425164744p:plain — parse-distance-tree-reconstruction-accuracy

論文にも記載がありますが、注目点として、どのグラフ（軌跡）も $k=64, 128$ で頭打ちになっています。これは、直感的には、k が大きくなれば、表現力が増え構文をより表現できるハズですが、 BERTBase, BERTLarge, ELMo の3モデルから推察すると、Bによる変換は、モデルによらず近似的に同じrank (最も良い精度になる次元）になると予想されます。

つまり、モデルによらず英語の構文を表現するベクトル空間の最小次元が一致する可能性があります。別の言い方をすると、英語の構文を表現するベクトル空間がいずれも同型になり得る（たぶん、位相同型＆線形同型になり得る）とも考えられます。なんとなく、完備化したら同型になる気がしてます（i.e. バナッハ空間として同型）。

簡易実験の結果と考察

入力を比較的容易に追加・変更できるdemo.py の実行結果（BERT-Large）を見てみます。

f:id:bci-oshita:20190426001808p:plain — demo-result

上２つは、github のサンプル文で、3番目は、ELMo の学習データの1番目の文、残りの下３つは、確認が容易になるように簡単な文として追加したものです。

I am a hero ! と、I am an expert ! は、同じ構文木になっても良さそうですが、そうはならなかったです。

なんとなく、冠詞（a、anなど）の扱いが微妙な印象があります。確かに、普通に考えても、a などの冠詞が複数登場する可能性が高いので、同じ単語ベクトルに対して距離やノルムが、一意に定まらないことが起因していそうです。

最後のI will go there の構文木は、違和感がない結果になっています。直感とは合わない構文木も生成されますが、埋め込まれたベクトルから線形変換のみで、木構造を復元できそうというのは、まったくあり得ないことではないように思えます。

感想

今回の論文は、非常にシンプルでわかりやすい提案手法と結果であった印象です。ベクトル空間から別のベクトル空間に写像することで、グラフ構造を埋め込めそうな予感を与えてくれる興味深いものでした。

まとめ

提案された structural probe は、2種類である
- distance ベース
- depth ベース
木構造の再構築は、距離行列を使った（つまり、全結合のグラフから）MSTアルゴリズムで、木構造を抽出する
- MST: Minimum Spanning Tree
木構造の再構築に対する指標は、UUAS （Undirected Unlabeled Attachment Score）
- 全ての文に対する、正解枝数 / 全枝数
- 若干、この定義でいいのかは、気になるところ。
UUASと各層の関係から、層の深さ（多さ）がタスクの分解能に対応しているようにも見える
UUASと次元数の関係から、64次元ぐらいで十分な構造の表現力を持ちうると示唆される
- これが、モデル依存なのかどうかは要検証
簡易実験の結果から、すごくシンプルな同じ木構造（構文木）になるべき文に対しても、異なる木構造として再現する
- これは、冠詞などのように、一つの文の中に複数回出現しうる単語が起因していると考えられる
- 同じ文で複数回出現すると、距離、ノルムが１意に定まらないことが起因している印象
ベクトル空間に、木構造（グラフ構造）を埋め込める可能性を示唆する、興味深い論文でした
- 現時点では、再現された木構造がまだ未熟、といった印象はぬぐえません。

ブレインズコンサルティング・テックブログ

あの論文を検証してみた！ - シリーズ第６回 - Structual Probe 論文

検証環境

本検証におけるアウトプット

コード

参考

スクリプト実行例

スクリプトの構成概要

experiment

distance ベース

depth ベース

run_experiment.py の構成概要

demo

demo の実行

BERT-Largeのmodel、vocabをダウンロード

run_demo.py の構成概要

概要

準備

The structural probe

最適化

木構造の復元方法

木構造の評価

Tree depth structural probe

（参考）CoNLL-U Format

グラフと考察

各層のUUAS

UUASと次元 $k$ の関係

簡易実験の結果と考察

感想

まとめ

参考リンク

検証環境

本検証におけるアウトプット

コード

参考

スクリプト実行例

スクリプトの構成概要

experiment

distance ベース

depth ベース

run_experiment.py の構成概要

demo

demo の実行

BERT-Largeのmodel、vocabをダウンロード

run_demo.py の構成概要

概要

準備

The structural probe

最適化

木構造の復元方法

木構造の評価

Tree depth structural probe

（参考）CoNLL-U Format

グラフと考察

各層のUUAS

UUASと次元の関係

簡易実験の結果と考察

感想

まとめ

参考リンク

UUASと次元 $k$ の関係